Approximating Global Contact-Implicit MPC via Sampling and Local Complementarity
Overview Video
TL;DR: We approximate global contact-implicit MPC (CI-MPC) by sampling global end effector locations, computing their local CI-MPC plans in parallel, and switching between contact-free and contact-rich modes.
Abstract
To achieve general-purpose dexterous manipulation, robots must rapidly devise and execute contact-rich behaviors. Existing model-based controllers are incapable of globally optimizing in real-time over the exponential number of possible contact sequences. Instead, recent progress in contact-implicit control has leveraged simpler models that, while still hybrid, make local approximations. However, the use of local models inherently limits the controller to only exploit nearby interactions, potentially requiring intervention to richly explore the space of possible contacts. We present a novel approach which leverages the strengths of local complementarity-based control in combination with low-dimensional, but global, sampling of possible end-effector locations. Our key insight is to consider a contact-free stage preceding a contact-rich stage at every control loop. Our algorithm, in parallel, samples end effector locations to which the contact-free stage can move the robot, then considers the cost predicted by contact-rich MPC local to each sampled location. The result is a globally-informed, contact-implicit controller capable of real-time dexterous manipulation. We demonstrate our controller on precise, non-prehensile manipulation of non-convex objects using a Franka Panda arm.
Uncut SE(3) Manipulation Videos
Loose tolerances: 5cm, 0.4rad (22.9 degrees)
73 consecutive SE(3) goals
Tight tolerances: 2cm, 0.1rad (5.7 degrees)
For our 3D jack example, we aggregate time-to-goal statistics across 4 continuous experiments containing 21, 16, 15, and 15 consecutive SE(3) goals. The above uncut videos depict these full-length experiments.
Uncut SE(2) Manipulation Videos
Tight tolerances: 2cm, 0.1rad (5.7 degrees)
For our planar push-T example, we aggregate time-to-goal statistics across 4 continuous experiments containing 56, 20, 20, and 10 consecutive SE(2) goals. The above uncut videos depict these full-length experiments.
Limitations of Local Models
Many CI-MPC methods use local models to approximate the dynamics in a real-time-capable manner. One example is Consensus Complementarity Control (C3), which represents the multi-contact dynamics as a linear complementarity system (LCS). An LCS captures the hybrid aspect of contact-rich dynamics but is fundamentally local.
LCS Views of Object Geometry
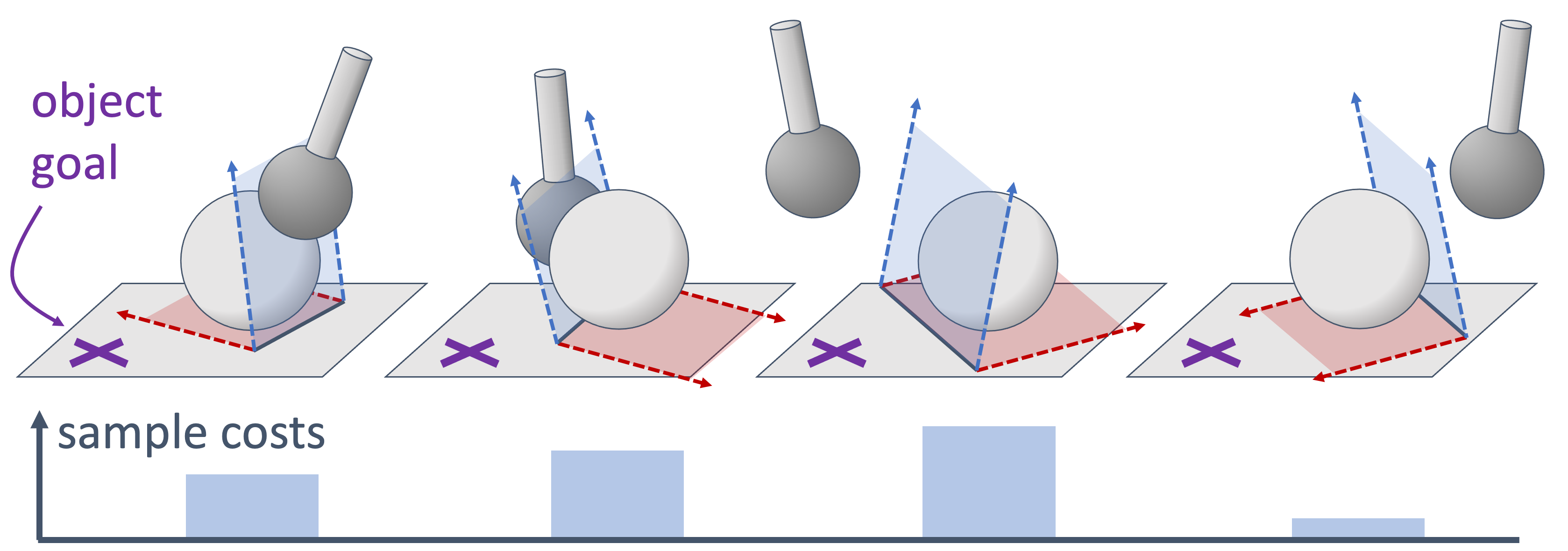
Loosely speaking, the LCS approximates object geometry as a set of hyperplanes coincident with and tangent to their witness points with respect to other geometries of interest. In the above example, a spherical end effector approaches a spherical object on a flat surface. The ground-object hyperplane is in red, while the robot-object hyperplane is in blue. A local controller built on LCS dynamics like C3 computes a contact-rich trajectory from a given initial configuration, which defines the LCS. With different initial configurations, the LCS is defined by different hyperplanes, and thus yields different contact-rich trajectories with different associated MPC costs. In the above example, four initial configurations of the end effector with respect to the object are shown. The rightmost LCS approximation allows the robot to most effectively foresee progressing the object toward the goal, and thus it has the lowest MPC cost.
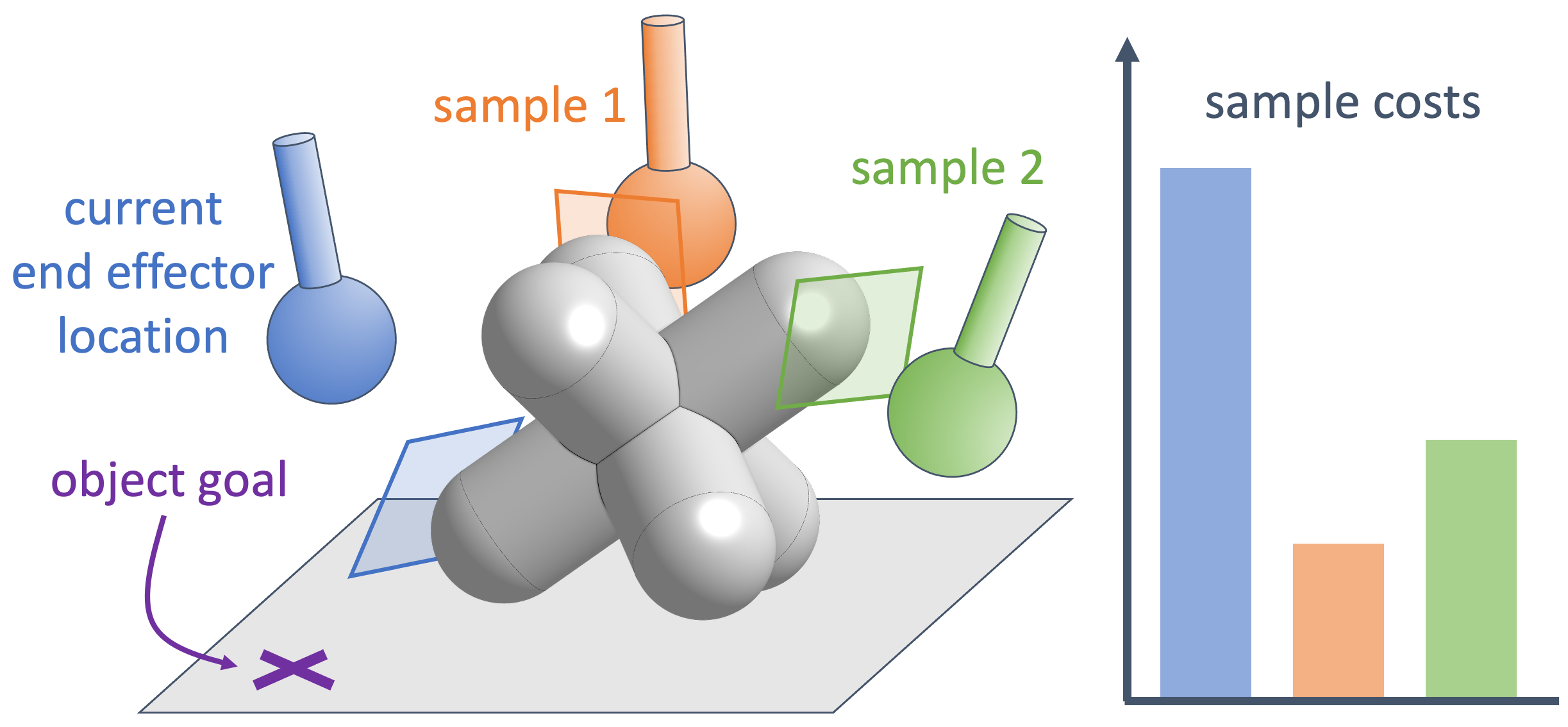
These LCS approimations are well-defined even for more complicated geometries, only requiring witness points between the object and other collision geometries. Above, the object-robot hyperplanes for three different end effector locations are shown, with sample costs on the right.
Our Algorithm: Inject Global Insights into Local Contact-Implicit Control

In this work, we extend the capabilities of C3 by injecting global insights into the local problem. While using an LCS model enables C3's real-time performance, its locality (described above) is problematic and motivates our approach. The key is to split the problem into an initial contact-free mode and a subsequent contact-rich mode. The contact-free mode explores globally, setting up the contact-rich mode in a region tractably handled by C3. To approximate the new bilevel optimization problem in real-time, we sample low-dimensional end effector locations at the mode switch. In closed-loop, our controller uses progress and cost metrics to autonomously switch between modes.
Implementation

Our controller is implemented in C++ within the Drake systems framework. In parallel, we consider 3 end effector samples (including the current end effector location) at every control loop. We connect our controller to an operational space controller (OSC), which tracks task-space commands specified by our policy at 8-12 Hz, via joint-level control at 1 KHz. We additionally integrate with Franka hardware and state estimators as in the control diagram above. Object state estimation uses FoundationPose running at 30Hz with a D455 RealSense RGBD camera. Our setup uses two computers: a computer with a 13th generation Intel Core i9-13900KF with 32 threads (for our sampling-based CI-MPC) and an NVIDIA GeForce RTX 4090 GPU (for FoundationPose), and an Intel i7-8700K processor (for our OSC and robot drivers) equipped with a real-time kernel for communicating with the Franka. Inter-computer communication occurs over LCM.
Numerical Results
| Mean ± σ [Min, Max] |
Time to Goal (s) within Pose Tolerances | |
|---|---|---|
| Tight: 2cm, 0.1 rad | Loose: 5cm, 0.4 rad | |
| Hardware SE(3) Jack (Ours) 67 trials |
109.20 ± 64.24 [17.40, 292.07] |
84.86 ± 60.54 [5.20, 257.74] |
| Simulation SE(3) Jack (Ours) 26 trials |
49.31 ± 30.35 [9.71, 124.70] |
33.84 ± 26.39 [7.97, 97.82] |
| Simulation SE(3) Jack (MJPC) 34 trials |
107.91 ± 112.38 [3.30, 567.69] |
68.00 ± 83.50 [1.51, 343.79] |
| Hardware SE(2) Push-T (Ours) 106 trials |
30.45 ± 13.11 [7.50, 79.43] |
17.43 ± 7.59 [3.86, 42.00] |
Comparison to MuJoCo MPC (MJPC)
Due to the inability to escape geometric local minima, C3 fails essentially 100% of the time on our tasks and thus is not compared. We compare with MuJoCo MPC (MJPC) with predictive sampling on the 3D jack task in simulation.
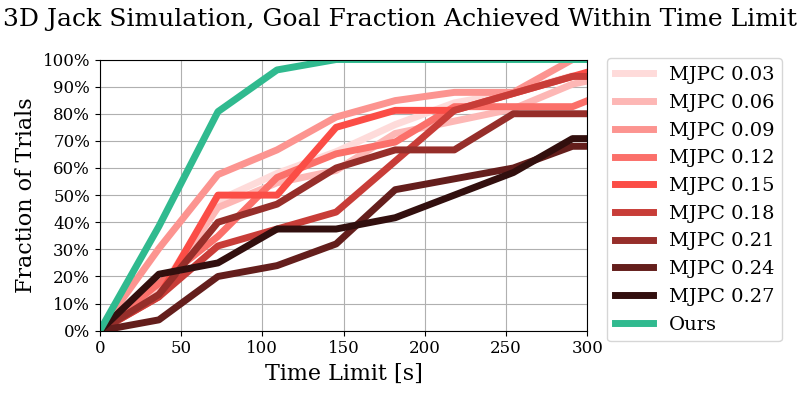
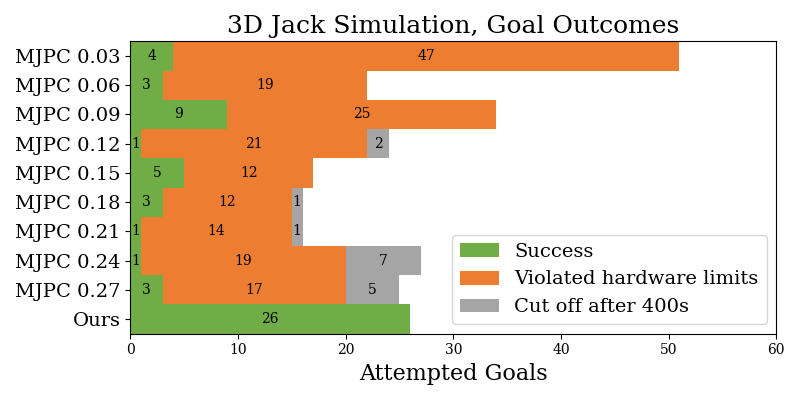
Our controller outperforms MJPC in simulation on our 3D jack example. Further, our controller satisfies Franka hardware limits (joint velocity/torque, workspace limits), while MJPC nearly always violates at least one. Given this high hardware limit violation rate, we did not feel safe deploying MJPC on the real robot. While impossible to compare against all possible MJPC weights, we put forth a best-faith effort in tuning and further investigated the role of end effector velocity cost weight, due to its role in the controller's speed. Increasing this cost weight makes MJPC less performant, yet does not prevent hardware limit violations.
Acknowledgments
This work was supported by a National Defense Science and Engineering Graduate (NDSEG) Fellowship, an NSF CAREER Award under Grant No. FRR-2238480, and the RAI Institute.
Citation
If you find this work useful, please consider citing: (bibtex)
@article{venkatesh2025approximating,
title={Approximating Global Contact-Implicit MPC via Sampling and Local Complementarity},
author={Sharanya Venkatesh* and Bibit Bianchini* and Alp Aydinoglu and William Yang and Michael Posa},
year={2025},
journal={arXiv preprint arXiv:2505.13350},
website={https://approximating-global-ci-mpc.github.io/}
}